Extracting the V matrix for MLMs
Notes to self (and anyone else who might find this useful). With the general linear mixed models (to simplify, I am just omitting super/subscripts):
$$Y = X\beta + Zu + e$$where we assume $u \sim MVN(0, G)$ and $e \sim MVN(0, R)$. $V$ is:
$$V = ZGZ^T + R$$Software estimates $V$ iteratively and maximizes the likelihood (the function of which depends on whether ML or REML is used). The value of $\beta$ can be obtained using:
$$\hat{\beta} = (X^TV^{-1}X)^{-1}X^TV^{-1}y$$.
I just wanted to figure out how to extract $V$ from the R output.
1. Manual method
Just using the sleepstudy dataset:
library(lme4)
data(sleepstudy)
nrow(sleepstudy) #total number of observations
[1] 180
dplyr::n_distinct(sleepstudy$Subject) #number of clusters
[1] 18
m1 <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)
summary(m1)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Reaction ~ Days + (Days | Subject)
Data: sleepstudy
REML criterion at convergence: 1744
Scaled residuals:
Min 1Q Median 3Q Max
-3.954 -0.463 0.023 0.463 5.179
Random effects:
Groups Name Variance Std.Dev. Corr
Subject (Intercept) 612.1 24.74
Days 35.1 5.92 0.07
Residual 654.9 25.59
Number of obs: 180, groups: Subject, 18
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 251.41 6.82 17.00 36.84 < 2e-16 ***
Days 10.47 1.55 17.00 6.77 3.3e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
Days -0.138
To obtain the $V$ matrix:
Z <- getME(m1, 'Z') #180 x 36
G <- bdiag(VarCorr(m1)) #2 x 2
G #the vcov matrix for RE
## 2 x 2 sparse Matrix of class "dsCMatrix"
## (Intercept) Days
## (Intercept) 612.1 9.6
## Days 9.6 35.1
R <- diag(sigma(m1)^2, nobs(m1)) #180 x 180
$G$ is a 2 $\times$ 2 matrix. Need to expand this based on the number of cluster/subjects.
Gm <- kronecker(diag(18), G)
Gm[1:6, 1:6] #just to show this
## 6 x 6 sparse Matrix of class "dgCMatrix"
##
## [1,] 612.1 9.6 . . . .
## [2,] 9.6 35.1 . . . .
## [3,] . . 612.1 9.6 . .
## [4,] . . 9.6 35.1 . .
## [5,] . . . . 612.1 9.6
## [6,] . . . . 9.6 35.1
V <- Z %*% Gm %*% t(Z) + R
Knowing $V$, we can put this together to get the fixed effects:
X <- model.matrix(m1)
y <- m1@resp$y
I will just make a function to put this together:
getFE <- function(X, V, y){
solve(t(X) %*% solve(V) %*% X) %*% t(X) %*% solve(V) %*% y
}
getFE(X, V, y)
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 251.4
## Days 10.5
fixef(m1) #the same
## (Intercept) Days
## 251.4 10.5
Doing this way is fine for simple, well arranged (sorted) datasets but can get more complicated with more levels of clustering (three or more levels). I had to create the Gm matrix.
2. More automated way:
After some Googling, I found this which shows how to make a more general function to construct that $V$ matrix. I just put this into a function which will make it easier to call and should work with more complicated RE specifications:
getV <- function(x){
var.d <- crossprod(getME(x, "Lambdat"))
Zt <- getME(x, "Zt")
vr <- sigma(x)^2
var.b <- vr * (t(Zt) %*% var.d %*% Zt)
sI <- vr * Matrix::Diagonal(nobs(x)) #for a sparse matrix
var.y <- var.b + sI
}
Just using the earlier example:
getFE(X, getV(m1), y) #works
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 251.4
## Days 10.5
3. Try it with simple three level data…
Just make a small dataset that is manageable (always helpful to be able to see the data). Five students with 3 teachers in 10 sch (or 15 students per school)
n1 <- 5; n2 = 3; n3 = 10
sch <- letters[1:10] #schoolid
tch <- 1:30 #teacherid
sch.cl <- rep(sch, each = n1 * n2) #cluster var
tch.cl <- rep(tch, each = n1)
set.seed(123)
e3 <- rep(rnorm(n1), each = n1 * n2)
e2 <- rep(rnorm(n2 * n1), each = n1)
x1 <- rnorm(n1 * n2 * n3)
e1 <- rnorm(n1 * n2 * n3)
y <- e3 + e2 + .5 * x1 + e1
dat <- data.frame(y, sch.cl, tch.cl, e3, e2, x1, e1)
dat[1:30, ]
y sch.cl tch.cl e3 e2 x1 e1
1 0.405 a 1 -0.56 1.715 -1.0678 -0.2154
2 1.111 a 1 -0.56 1.715 -0.2180 0.0653
3 0.608 a 1 -0.56 1.715 -1.0260 -0.0341
4 2.919 a 1 -0.56 1.715 -0.7289 2.1285
5 0.101 a 1 -0.56 1.715 -0.6250 -0.7413
6 -2.039 a 2 -0.56 0.461 -1.6867 -1.0960
7 0.357 a 2 -0.56 0.461 0.8378 0.0378
8 0.288 a 2 -0.56 0.461 0.1534 0.3105
9 -0.232 a 2 -0.56 0.461 -1.1381 0.4365
10 0.069 a 2 -0.56 0.461 1.2538 -0.4584
11 -2.676 a 3 -0.56 -1.265 0.4265 -1.0633
12 -0.710 a 3 -0.56 -1.265 -0.2951 1.2632
13 -1.728 a 3 -0.56 -1.265 0.8951 -0.3497
14 -2.252 a 3 -0.56 -1.265 0.8781 -0.8655
15 -1.651 a 3 -0.56 -1.265 0.8216 -0.2363
16 -0.770 b 4 -0.23 -0.687 0.6886 -0.1972
17 0.470 b 4 -0.23 -0.687 0.5539 1.1099
18 -0.863 b 4 -0.23 -0.687 -0.0619 0.0847
19 -0.316 b 4 -0.23 -0.687 -0.3060 0.7541
20 -1.607 b 4 -0.23 -0.687 -0.3805 -0.4993
21 -0.809 b 5 -0.23 -0.446 -0.6947 0.2144
22 -1.104 b 5 -0.23 -0.446 -0.2079 -0.3247
23 -1.214 b 5 -0.23 -0.446 -1.2654 0.0946
24 -0.487 b 5 -0.23 -0.446 2.1690 -0.8954
25 -1.383 b 5 -0.23 -0.446 1.2080 -1.3108
26 2.430 b 6 -0.23 1.224 -1.1231 1.9972
27 1.393 b 6 -0.23 1.224 -0.4029 0.6007
28 -0.491 b 6 -0.23 1.224 -0.4667 -1.2513
29 0.773 b 6 -0.23 1.224 0.7800 -0.6112
30 -0.233 b 6 -0.23 1.224 -0.0834 -1.1855
m2 <- lmer(y ~ x1 + (1|sch.cl/tch.cl), data = dat)
summary(m2)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: y ~ x1 + (1 | sch.cl/tch.cl)
Data: dat
REML criterion at convergence: 490
Scaled residuals:
Min 1Q Median 3Q Max
-2.5495 -0.5604 -0.0782 0.5296 2.0960
Random effects:
Groups Name Variance Std.Dev.
tch.cl:sch.cl (Intercept) 1.226 1.107
sch.cl (Intercept) 0.420 0.648
Residual 0.981 0.991
Number of obs: 150, groups: tch.cl:sch.cl, 30; sch.cl, 10
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 0.3759 0.2991 8.9956 1.26 0.24045
x1 0.3588 0.0922 124.7229 3.89 0.00016 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
x1 0.005
Z <- getME(m2, "Z") #n x (sch + tch; just intercepts)
dim(Z)
[1] 150 40
image(Z[1:30,]) #just showing the Z matrix for the first 30 obs
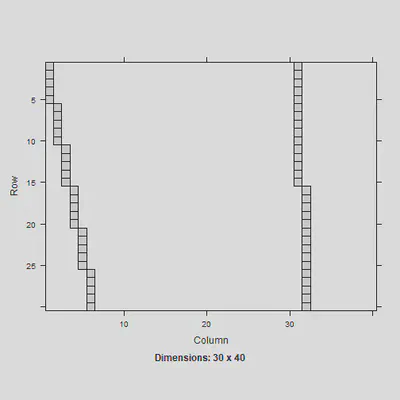
The $Z$ design matrix is different now since there are more than two levels. This needs to be multiplied by the $Gm$ matrix to follow:
G <- bdiag(VarCorr(m2))
G #how should G then be formed for the Gm?
2 x 2 sparse Matrix of class "dsCMatrix"
[1,] 1.23 .
[2,] . 0.42
Intercept variance on upper left is for teachers and lower right is for schools. Constructing the matrix is relatively straightforward. Doing this manually.
a1 <- kronecker(diag(30), 1.226473) #for teachers
a2 <- kronecker(diag(10), .4201496) #for schools
Gm <- bdiag(a1, a2) #stacking as a diagonal matrix
dim(Gm)
## [1] 40 40
image(Gm)
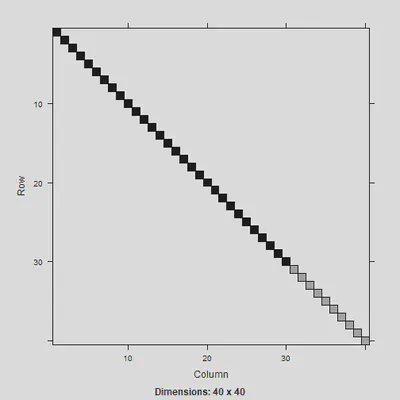
Can then use this to create the $V$ matrix:
V <- Z %*% Gm %*% t(Z) + diag(sigma(m2)^2, nobs(m2))
X <- model.matrix(m2)
y <- m2@resp$y
getFE(X, V, y) #compute our fixed effects
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 0.376
## x1 0.359
fixef(m2) #the same
## (Intercept) x1
## 0.376 0.359
If we use our getV function, this just works too which much less hassle!
getFE(X, getV(m2), y)
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 0.376
## x1 0.359
4. Throw in random slopes
The above will only work if the structure of $Z$ and $G$ are simple. If data are not sorted, that may not work.
library(mlmRev)
library(dplyr)
data(star)
set.seed(123)
konly <- filter(star, gr == 'K') %>% sample_frac(.2) #just selecting a few
#so the Z matrix can be seen
m3 <- lmer(read ~ cltype + sx + (sx|sch/tch), data = konly)
X <- model.matrix(m3)
y <- m3@resp$y
Vm <- getV(m3)
getFE(X, Vm, y)
4 x 1 Matrix of class "dgeMatrix"
[,1]
(Intercept) 438.91
cltypereg -5.92
cltypereg+A -2.21
sxF 2.05
fixef(m3) #the same!
(Intercept) cltypereg cltypereg+A sxF
438.91 -5.92 -2.21 2.05
Look at the $G$ matrix:
bdiag(VarCorr(m3))
## 4 x 4 sparse Matrix of class "dsCMatrix"
##
## [1,] 141.8 -10.118 . .
## [2,] -10.1 0.722 . .
## [3,] . . 153.9 -6.399
## [4,] . . -6.4 0.266
The Z matrix is a mess!
Z <- getME(m3, 'Z')
image(Z)
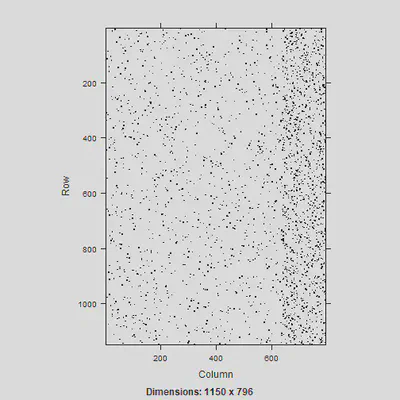
You can compute the $V$ matrix per cluster but in this example, just wanted to get the overall matrix.
–END